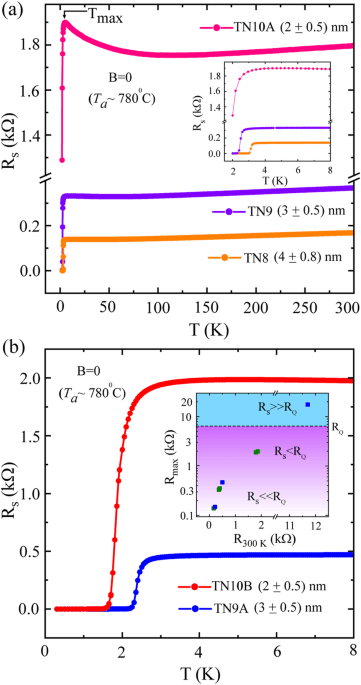
The temperature dependent sheet resistance Rs(T) measurements for five representative TiN samples of thickness 2–4 nm are presented in Fig. 1. Three samples measured down to 2 K are shown in Fig. 1a and the rest two measured down to 300 mK take place in Fig. 1b. With reduction in thickness, the normal state resistance (RN) increases and the transition temperature (Tc) decreases. Here, Tc corresponds to the temperature at which the derivative dRs/dT becomes maximum. The Tc values closely match with their respective mean field transition temperature Tc0 as obtained from the quantum corrections to the conductivity (QCC) theories31,34. Further, while cooling down from room temperature, an upturn with a resistance maximum Rmax appears for all the samples just before the superconducting onset indicating a weakly localized metallic state34. The appearance of the resistance peak Rmax at the temperature Tmax is shown by the arrows in Fig. 1a for the sample TN10A and in Supplementary Fig. 1 for samples TN9 & TN8. It is evident that with reduction in thickness, samples become more disordered and more localized as indicated by the increased RN and the steeper slope for the negative dRs/dT region of the resistance upturn, respectively.
Based on the lowest achievable measurement temperature, two sets of samples are presented in (a) and in the main panel of (b). a Rs(T) for the temperature range from room temperature down to 2 K for three representative samples from the first set. Inset: the same set of Rs(T) but for a selected range of temperature to highlight the metal-superconductor transition region. b Rs(T) near the transition region for other two samples from the second set measured down to 300 mK. Here, the samples TN10A & TN10B were prepared in one single run and the samples TN9 & TN9A were grown in the same batch. Inset: The resistance Rmax, measured at Tmax as shown by the arrow in Fig. 1a just above the superconducting onset, is plotted against the resistance measured at room temperature (R300 K) for all the samples. The dashed horizontal line, separating the blue and purple shaded regions, refers the quantum resistance RQ. The resistance values for the samples are compared with respect to the quantum resistance.
In the inset of Fig. 1b, the RN values for all the samples presented in this article and in Supplementary Fig. 2 (Supplementary Note 1) are summarized with respect to the quantum resistance RQ which is denoted by the horizontal dashed line separating the two shaded regions in cyan and purple. As for the reference of RN, the resistance Rmax is plotted against the room temperature resistance R300 K. Here, the selected samples offer more than two orders of change in the RN from ~140 Ω to ~18 kΩ. The wide variations in RN are obtained by tuning the thickness and the annealing temperature (Ta) during the growth process. Two different temperatures for Ta, 780 °C and 820 °C, are considered here, and the resistance values for the corresponding samples are shown in olive-green and blue rectangles, respectively. Comparing the resistance with respect to RQ, the samples with resistance less than 500 Ω are considered here as weakly disordered (RS≪RQ), the samples with resistance more than 1.5 kΩ are considered as moderately disordered (RS < RQ) and the samples with resistance much higher than RQ are considered as strongly disordered (RS≫RQ).
Emergence of multiple crossing points in magnetoresistance isotherms
The magnetic-field and temperature dependent sheet resistance Rs(B,T) measurements for the samples measured down to 2 K are shown in Fig. 2 where the left panel represents the Rs(T) measured under different field and the right panel displays the magnetoresistance isotherms Rs(B). The sample thickness varies in descending order from the top to the bottom. For comparison among the samples, the variations of Rs(T) with field are placed in equivalent scaling as evident by their normalized resistance Rs/Rmax. With increasing field, a resistance plateau indicating a field induced SMT (or weakly localized metallic transition)18 is observed for the 4 nm (TN8) and 3 nm (TN9) thick samples, whereas, a relatively strong upturn indicating a SIT or superconductor to weak insulator transition20 appears for the thinnest sample TN10A (2 nm). Further, a selective region of the measured Rs(B) isotherms from each of the samples TN8, TN9 & TN10A is highlighted in Fig. 2b, d, f, respectively. In contrast to the conventional single point crossing, the Rs(B) isotherms, measured between 2 and 5 K with 0.1 K interval, display a series of crossing points (shown in black filled diamonds) that form a continuous line of SMT/SIT critical points. The appearance of a continuum of MCPs hints towards the existence of QGS at very low temperature (\(T\to 0\)) where the critical exponents product \(z\nu\) diverges15,16,21. Furthermore, a quantitative analysis on the relative span ΔBc/ΔT covered by the MCPs is done with respect to the sample thickness. Here, ΔBc is the extent in magnetic field for a specific range of temperature ΔT. The values of ΔBc/ΔT for samples TN8 (4 nm), TN9 (3 nm) and TN10A (2 nm) are found as 0.306 T/K, 0.446 T/K and 0.896 T/K, respectively. Thus, thickness reduction leads to an enhancement in the relative span of the MCPs and from the trend, one can expect a single crossing point in relatively thicker samples. A similar trend is observed in Supplementary Fig. 3 (Supplementary Note 2) for the samples TN4 (4 nm) and TN5A (3 nm) that are annealed at 820 °C.
Field dependent Rs(T) for (a) TN8, (c) TN9A & (e) TN10A and isothermal magnetoresistance [Rs(B)] demonstrating multiple crossing points in the temperature range from 2 K to 5 K for (b) TN8, (d) TN9A & (f) TN10A. Here, the black solid diamonds mark the crossing points (Bc) for three consecutive Rs(B) isotherms measured with an interval of 0.1 K in the temperature. Double sided arrows show the span ΔBc in the field covering the multiple crossing region for the temperature window of 2–5 K. Here, it should be noted that a resistance change of about ~ 3 Ω between Rs(T) and Rs(B) for the sample TN8 occurs due to thermal cycling during the measurements.
Figure 2 indicates that the field extent covered by MCPs increases with increasing disorder and hence the randomness in the critical behavior gets stronger with increasing disorder. In Fig. 3, we present Rs(B,T) measurements for a highly disordered sample (TN6) with RN≫RQ. The zero-field Rs(T) measured from room temperature down to 2 K as shown in Fig. 3a clearly shows a non-metallic behavior in the normal state above the Tmax with negative dRS/dT in the whole temperature range from 300 K down to Tmax. Here, the upward slope gets much steeper just above the Tmax while approaching the Tmax from higher temperature side and a resistance peak Rmax appears at the Tmax. This leads to a much higher Rmax than the resistance R300 K measured at 300 K. Further, for T < Tmax, a resistance drop of about 25% of the Rmax is observed down to 2 K. The evolution of the transition region of the Rs(T) under magnetic field as shown in the inset of Fig. 3a presents a transition from superconducting to insulating regime upon the field variation from 2 T to 4 T. Further, Fig. 3b presents Rs(B) isotherms for the temperature window of Tmax to 2 K where a continuum of MCPs (shown by the black filled diamonds) is clearly evident. The relative span (ΔBc/ΔT) of the MCPs appears as ~2.37 T/K which is indeed much higher than the samples shown in Fig. 2 with relatively low RN. Therefore, MCPs are observed in ultrathin TiN (≤4 nm) samples spanning in wide range of disorder which indicates the existence of MCPs in both types of field induced QPTs SMT and SIT.
The magnetoresistance Rs(B) data is extracted from the field dependent Rs(T) by the inverse matrix method. The thickness of the sample is (2 ± 0.5) nm and the annealing temperature (Ta) during its growth was ~ 820 °C. Here, the increased resistance is caused by the formation of elemental Si at Ta ~ 820 °C in addition to TiN. a Zero-field Rs(T) measured from room temperature down to 2 K. Inset: Rs(T) measured under external magnetic field applied perpendicular to the sample plane. b Isothermal Rs(B) obtained for the temperature window of 2–3.2 K. The black filled diamonds represent the crossing points between the neighboring isotherms in small temperature intervals.
Emergence of quantum Griffiths singularity
The continuum of MCPs observed in Rs(B,T) measured down to 2 K (shown in Fig. 2, 3) indicates towards the existence of QGS in these samples at zero temperature limit19 where the observation of diverging critical exponent \(z\nu\) provides the solid evidence of QGS28. Consequently, two samples TN9A (~3 nm) and TN10B (~2 nm) exhibiting field-induced SMT & SIT, respectively, are measured down to 300 mK. The Rs(B,T) measurements for TN9A are presented in Fig. 4. With increasing magnetic field from 3.5 T to 3.75 T in the field dependent Rs(T) as shown in Fig. 4a, transition from superconducting to weakly localized metallic state is observed at the lowest measurement temperature. Further, Fig. 4b presents the Rs(B) isotherms measured in the temperature interval 0.3 K ≤ T ≤ 3 K where the neighboring Rs(B) isotherms cross at different critical fields (shown in black diamonds) that form a continuous line of MCPs indicating the existence of QGS19,28. This continuum of MCPs spans over a wide range of temperature and magnetic field. The temperature dependence of the crossing field Bc(T) is shown in the inset of Fig. 4b. Here, the average temperature is considered at each crossing point and the error bars represent the range.
a A selected region of field dependent Rs(T) measured under perpendicular magnetic fields from 0 to 4.5 T in 0.25 T steps. b Isothermal Rs(B) measured in the temperature window of 0.3 K ≤ T ≤ 3 K. The magnetoresistance isotherms are measured with a temperature interval of 0.05 K between two neighboring isotherms from 0.3 K to 0.85 K, with 0.1 K interval from 0.85 K to 1.85 K and with 0.25 K interval from 2 K to 3 K. The crossing points are shown by the black diamonds. Inset: The crossing field (Bc)—temperature (T) phase boundary near the quantum superconductor-to metal transition. The red curve is the fit using Eq. (5) with \({B}_{c}^{* }\), \({u}\) and \(p\) as adjustable parameters and the characteristic temperature T0 fixed at 4.41 K (see the text for details). c Divergent behavior of critical exponent \(z\nu\) as a function of magnetic field. The \(z\nu\) values are obtained through finite size scaling (FSS) analysis for a set of adjacent magnetoresistance isotherms. The solid red curve is the fit based on activated scaling law using Eq. (2) and two black dashed lines represent \(z\nu =1\) (horizontal) & \({B}_{c}^{* }=3.78{T}\) (vertical). d Sheet resistance as a function of the scaling parameter \(\delta {\left({{{{\mathrm{ln}}}}}\left({T}_{0}/T\right)\right)}^{1/\nu \psi }\) related to the activated dynamical scaling as described in Eq. (4) for the temperature span 0.3 K ≤ T ≤ 1.75 K. Error bars denote the temperature range for a set of magnetoresistance isotherms.
The existence of QGS can be established by the divergence of critical exponent \(z\nu\) upon approaching the QPT at T → 0 and B → \({B}_{c}^{* }\), where \({B}_{c}^{* }\) is the characteristic critical field15,16,21. Here, the critical exponent \(z\nu\) is obtained by adopting the finite size power law scaling (FSS) analysis as is generally used for a continuous QPT associated with a fixed single QCP7. Under the power law scaling, the temperature and magnetic field dependent sheet resistance Rs(B,T) near a field induced QPT can be described as7,
$${R}_{s}(B,T)={R}_{s}^{c} \, f(\delta {T}^{-1/z\nu })$$
(1)
where, \(\delta =|B-{B}_{c}|\) is the distance from the critical field \({B}_{c}\), \({R}_{{{{{{\rm{s}}}}}}}^{{{{{{\rm{c}}}}}}}\) is the sheet resistance at the critical point and \({f}(x)\) is the scaling factor with \(f\left(0\right)=1\). \(z\) and \(\nu\) are the dynamical and corelation length critical exponents, respectively. To perform the FSS analysis on the Rs(B,T) data shown in Fig. 4b, a set of three adjacent Rs(B) isotherms crossing at a particular critical field Bc in each small temperature interval is considered for extracting \(z\nu\) values by using the power law scaling in Eq. (1). The detailed FSS analysis is illustrated in Supplementary Figs. (4)–(6) in the Supplementary Note 3. The extracted \(z\nu\) values are plotted against the critical fields in Fig. 4c. Initially, zν increases slowly with magnetic field from 3 K down to ~ 1.55 K, with further lowering temperature, \(z\nu\) increases rapidly with field and shows a diverging behavior while approaching the characteristic critical field \({B}_{c}^{* }\). This reflects an activated scaling behavior of \(z\nu\) with respect to the field near the characteristic critical field \({B}_{c}^{* }\) and is expressed as35,
$${z\nu \, \approx \, C(B-{B}_{c}^{* })}^{-\upsilon \psi },$$
(2)
where C is a constant and \(\upsilon =1.2\) & ψ = 0.5 are the corelation length exponent and the tunneling exponent associated with the 2D infinite-randomness fixed critical point (IRFCP), respectively35,36,37. The activated scaling law is in good agreement with the experimental data as shown by the red solid curve in Fig. 4c which yields \({B}_{c}^{* }\) = 3.78 T. This indicates towards the existence of IRFCP justifying the presence of QGS in the sample.
Further, a QPT governed by an IRFCP can be described by a direct activated dynamical scaling as a whole where the infinite-randomness critical exponent \(\upsilon \psi\) can replace the critical exponent \(z\nu\) associated with the conventional power law scaling. Here, at \(T\to 0\) the critical exponent products from power law scaling (zν) and activated dynamical scaling (\(\upsilon \psi\)) are related as28,
$$\left(\frac{1}{z\nu }\right)=\left(\frac{1}{\upsilon \psi }\right)\cdot \frac{1}{ln({T}_{0}/T)}$$
(3)
where the exponent \(\upsilon \psi\) (\(\upsilon\) is the corerelation length critical exponent and \(\psi\) is the tunneling exponent) represents the universality class of the QPT associated with IRFCP. The fit using Eq. (3) to the temperature dependent \(z\nu\) (shown in Supplementary Fig. 7 in the Supplementary Note 4) leads to the characteristic temperature T0 and the critical exponent \(\upsilon \psi\) which are used as free parameters. Further, Eq. (3) indiates a diverging \(z\nu\) while approaching to \(T\to 0\), confirming the QCP is of IRFCP type where physical quantities can be described by the direct activated dynamical scaling. Consequently, the sheet resistance Rs can be expressed as28,
$${R}_{s}\left(\delta ,{{{{\mathrm{ln}}}}}\frac{{T}_{0}}{T}\right)=\Phi \left[\delta {\left({{{{\mathrm{ln}}}}}\frac{{T}_{0}}{T}\right)}^{1/\upsilon \psi }\right]$$
(4)
where, \(\delta =\left|{B}_{c}-{B}_{c}^{* }\right|/{B}_{c}^{* }\) is the distance from the critical field \({B}_{c}^{* }\) associated to the IRFCP and \(\Phi\) corresponds to the scaling function. Here, T0 and \(\upsilon \psi\) are the same as have been used in Eq. (3). Further, the crossing field Bc(T) near the transition is also expected to follow the activated dynamical scaling with irrelevant scaling correction as28,
$${B}_{c}\left(T\right)={B}_{c}^{* }\times \left[1-u{\left({{{{\mathrm{ln}}}}}\frac{{T}_{0}}{T}\right)}^{-p}\right]$$
(5)
with the exponent \(p=\frac{1}{\upsilon \psi }+\frac{\omega }{\psi }\) and u is the leading irrelavant scaling variable responsible for the correction to the scaling. \(\omega\) is the associated irrelevant exponent which is always positive22. The red solid curve in the inset of Fig. 4b represents the fit to the Bc(T) phase boundary using Eq. (5) where \({B}_{c}^{* }\), \(u\) and \(p\) are considered as the fitting parameters. T0 = 4.41 K and \(\upsilon \psi =0.63\) are obtained from the fit using Eq. (3) [Supplementary Fig. 7a in the Supplementary Note 4]. Here, \(\upsilon \psi =0.63\) closely matches with the theoretically predicted value of ~ 0.6 with \(\upsilon \sim 1.2\) & ψ ∼ 0.535,36,37. The best fit values for \({B}_{c}^{* }\), \(u\) and \(p\) are obtained as (3.77 ± 0.02) T, (0.115 ± 0.007) and (1.92 ± 0.15), respectively.
Further, in Fig. 4d, the direct activated dynamical scaling using Eq. (4) has been applied on a set of Rs(B) isotherms and the best collapse is obtained for \({B}_{c}^{* }=3.77{{{{{\rm{T}}}}}}\), T0 = 4.56 ± 0.23 K and \(\upsilon \psi =0.63\) in the temperature interval 0.3 K ≤ T ≤ 1.75 K. Here, \({B}_{c}^{* }\) is obtained by minimizing the variance in magnetoresistance isotherms when plotted against the scaling parameter18,28. The same value for \({B}_{c}^{* }\) is obtained from the phase boundary fitting of Bc(T) using Eq. (5) [inset of Fig. 4b]. Furthermore, \({B}_{c}^{* }=3.77{{{{{\rm{T}}}}}}\), agrees closely to 3.78 T which is obtained from the fit to the field dependence of \(z\nu\) using Eq. (2) [shown in Fig. 4b]. The characteristic temperature T0, used as an adjusting parameter to achieve the best collapse, is obtained as 4.56 ± 0.23 K which is close to the temperature 4.41 K as found from the fit of \(z\nu\) versus temperature using Eq. (3) (Supplementary Fig. 7 in the Supplementary Note 4). It is observed in Fig. 4d that for large values of the scaling parameter away from \({B}_{c}^{* }\), the scaling collapse starts to break down at ~ 4.29 T and ~1.85 T, for the upper and lower branches, respectively. These breakdowns can be attributted to the negligible quantum fluctuations occuring in the normal state at high magnetic field (upper branch) and in the superconducting state at very low magnetic field and low temperature (lower branch)18,28. It should be noted that the temperature window of 0.3 K ≤ T ≤ 1.75 K remains the same for (i) the direct activated scaling of the MR isotherms using Eq. (4) [in Fig. 4d], (ii) the Bc(T) phase boundary fitting using Eq. (5) [in the inset of Fig. 4(b)] and (iii) the \(z\nu\) vs. temperature fit using Eq. (3) [in Supplementary Fig. 7 in the Supplementary Note 4]. However, at high temperature, the quantum fluctuation becomes insignificant compared to the thermal fluctuations and the data set starts to deviate from the activated scaling.
Next in Fig. 5, we present the Rs(B,T) measurements carried out at temperature down to 300 mK for a more resistive (RN ~ 2 kΩ) sample TN10B (~2 nm) [shown in Fig. 1b] with weak insulating background where the formation of rare ordered superconducting puddles (Griffiths regions) via long-range Josephson coupling becomes more challenging compared to a metallic background. A selected region from the set of Rs(T), measured under fixed perpendicular fields from 0 to 5 T in 0.25 T steps, is shown in Fig. 5a. The trace of superconductivity with positive downward slope is observed for field up to 3.75 T. But, a clear upward transition with negative slope (dRs/dT < 0) occurs for an increased field of 4 T. Here, as the RN is lower than the RQ, the logarithmic derivative of the sheet conductance \(\left({\sigma }_{s}=1/{R}_{s}\right)\) is considered for examining the state for B ≥ 4 T. Though dRs/dT is negative but often this does not ascertain whether a sample is metallic or insulating18,38. It is shown that the logarithmic derivative of sheet conductance \(w={{{{{\rm{dln}}}}}}{\sigma }_{s}/{{{{{\rm{dln}}}}}}T\) at zero-temperature limit (\(T\to 0\)) is more sensitive than the derivative dRs/dT in determining whether a sample is metallic or insulating. For \({w} \, > \, 0\), a positive value of dw/dT indicates a metallic state whereas, a negative value of dw/dT indicates the sample to be very likely insulating39. In the inset of Fig. 5a, \(w={{{{{\rm{dln}}}}}}{\sigma }_{s}/{{{{{\rm{dln}}}}}}T\) corresponding to the Rs(T) measured under 4 T is plotted against T1/2. Here, \(w\) is positive and towards the lowest measurement temperature \(w\) increases with decreasing temperature leading to a negative value of\(\,{{{{{\rm{d}}}}}}w/{{{{{\rm{d}}}}}}T\). This indicates a field induced superconducting to insulating quantum phase transition (SIT) at zero-temperature limit for B ≥ 4 T. The insulating phase near the transition has been investigated further by Rs(B) isotherms measured at low temperature down to 300 mK and for a magnetic field up to 10 T. The corresponding magnetoresistance (MR) data is shown in Supplementary Fig. 10b in the Supplementary Note 6 which unveils a broad resistance peak for B ≥ 4 T. The appearance of resistance peak near the transition indicates the field-induced localization of Cooper pairs2,29,40,41. However, as the RN is much lower than the quantum resistance RQ of Cooper pairs, a parallel contribution from fermionic channel of quasiparticles is most likely to be present in addition to the bosonic contribution from localized Cooper pairs. Further, the logarithmic temperature dependence of the conductance [Supplementary Fig. 10c, d in the Supplementary Note 6] at higher field confirms the fermionic scenario5,34,42,43.
a A selected region of Rs(T) measured under perpendicular magnetic fields from 0 to 5 T in 0.25 T steps. Inset: Logarithmic derivative of sheet conductance (dlnσs/dlnT) vs. T1/2 obtained from the Rs(T) measured under 4 T field. b A detailed view of isothermal Rs(B) measured in the temperature window of 0.3 K ≤ T ≤ 3 K. The black diamonds represent the crossing points. Inset: The crossing field (Bc) – temperature (T) phase boundary near the quantum superconductor-to metal (SMT) transition. The red curve is the fit using Eq. (5) with \({{{{{{\rm{B}}}}}}}_{{{{{{\rm{c}}}}}}}^{* }\), \({{{{{\rm{u}}}}}}\) and \({{{{{\rm{p}}}}}}\) as adjustable parameters while the characteristic temperature T0 was fixed at 3.11 K (see the text for details). c Field-dependence of the critical exponent product zν which shows diverging behavior with magnetic field while approaching the characteristic critical field \({{{{{{\rm{B}}}}}}}_{{{{{{\rm{c}}}}}}}^{* }\) at the lowest measurement temperature. The zν values are obtained through finite size scaling (FSS) analysis for a set of adjacent magnetoresistance isotherms in each small interval of temperature. The solid red curve is the fit based on the activated scaling law using Eq. (2). The black dashed lines represent \({{{{{\rm{z}}}}}}{{{{{\rm{\nu }}}}}}=1\) (horizontal) & \({{{{{{\rm{B}}}}}}}_{{{{{{\rm{c}}}}}}}^{* }=4.03{{{{{\rm{T}}}}}}\) (vertical). The horizontal dashed-dotted broken line indicates a plateau region where \({{{{{\rm{z}}}}}}{{{{{\rm{\nu }}}}}}\) remains almost unchanged with changing magnetic field in the high temperature regime. d Sheet resistance as a function of the scaling parameter \({{{{{\rm{\delta }}}}}}{\left({{{{\mathrm{ln}}}}}\left({{{{{{\rm{T}}}}}}}_{0}/{{{{{\rm{T}}}}}}\right)\right)}^{1/{{{{{\rm{\nu }}}}}}{{{{{\rm{\psi }}}}}}}\) related to the activated dynamical scaling as described in Eq. (4) for the temperature span of 0.3 K ≤ T ≤ 1.75 K. Error bars denote the temperature range for a set of magnetoresistance isotherms.
Further, a detailed view near the field induced transition to the insulating state is shown in Fig. 5b by the Rs(B) isotherms measured in the temperature interval 0.3 K ≤ T ≤ 3.0 K. A continuum of MCPs (shown by the black diamonds) is evident. The phase boundary as represented by the temperature dependent crossing field Bc(T) is displyed in the inset of Fig. 5b. The red solid curve represents the activated dynamical fit using Eq. (5) for the temperature range 0.3 K ≤ T ≤ 1.75 K with T0 = 3.11 K and \(\upsilon \psi =0.62\) as obtained from the fit using Eq. (3) to the temperature dependent \(z\nu\) (Supplementary Fig. 7b in the Supplementary Note 4). The critical field \({B}_{c}^{* }\) is obtained as 4.03 ± 0.02 T. The best fit values for the parameters \(u\), \(p\) and the critical field \({B}_{c}^{* }\) are obtained as 0.031 ± 0.006, 2.15 ± 0.26 and 4.03 ± 0.02 T, respectively.
The field dependent \(z\nu\) is plotted in Fig. 5(c) which indicates a diverging \(z\nu\) while approaching the characteristic critical field \({{B}}_{c}^{* }\) at the low temperature limit. The experimental data is in good agreement with the activated scaling law as described by the red solid curve using Eq. (2) indicating towards the existence of IRFCP transition which justifies the presence of QGS in the systems. The best fit value for the characteristic field \({B}_{c}^{* }\) is obtained as 4.03 T. Further in Fig. 5d, a direct activated dynamical scaling using Eq. (4) is performed on the Rs(B,T). Here, the best collapse is observed for \({{B}}_{c}^{* }=4.0{{{{{\rm{T}}}}}}\) in the temperature range 0.3 K ≤ T ≤ 1.75 K with \(\upsilon \psi\) fixed at the value of 0.62. The best collapse, obtained by using the characteristic temperature T0 as an adjusting parameter, leads to T0 = 3.27 ± 0.25 K. The critical field \({{B}}_{c}^{* }=4.0{{{{{\rm{T}}}}}}\) is very close to the value of 4.03 T which is obtained from the phase boundary fitting of Bc(T) [inset of Fig. 5b] as well as from the activated scaling law as presented in Fig. 5c. Further, the characteristic temperature T0 is in good agreement too with the value obtained from the temperature dependence of \(z\nu\) shown in Supplementary Fig. 7b in the Supplementary Note 4. Here, the scaling collapse breaks down at high temperature and at fields far from the critical field \({{B}}_{c}^{* }\) due to the diminishing quantum fluctuations28.
Here, it is noteworthy to mention that Eq. (4) associated with the direct activated dynamical scaling of the MR isotherms predicts a single critical point \({B}_{c}^{* }\) which does not account for the temperature dependence of the crossing fields as observed by the MCPs. The scaling behaviors, shown in Fig. 4d and in Fig. 5d, confirm the existence of a single critical point in the magnetic field for a wide range of temperature from 300 mK to about 1.75 K for both the samples TN9A and TN10B. Further, Eq. (3) indicates a diverging behavior of the critical exponent \(z\nu\) with temperature at \(T\to 0\) and the corresponding fit shown in Supplementary Fig. 7 establishes the diverging behavior of \({z}\nu\) at low temperature. These observations confirm the QPT to be governed by an IRFCP. However, there is a clear difference in the temperature dependent critical field Bc(T) for these two samples TN9A (SMT category) and TN10B (SIT category). For the former, the critical field moves towards upward direction while approaching the zero-temperature limit [inset of Fig. 4b], wheras, for the latter, Bc increases initially with decreasing temperature in the high temperature regime (\(T \, \gtrsim \, 1\,{{{{{\rm{K}}}}}}\)) but finally it tends to saturate around \({B}_{c}^{* }\,(4.03\,{{{{{\rm{T}}}}}})\) as the temperature approaches to 0 K [inset of Fig. 5b]. The upward trend of \({B}_{c}(T)\) as observed for TN9A is similar to the other reported SMT systems exihibiting QGS15,18,20,24,25,26, whereas, a saturating Bc at zero-temperature limit is one of the features observed in systems showing SIT20. The differences in the behavior of Bc at \(T\to 0\) might be related to the different Josephson interaction strength among the superconducting puddles with insulating & metallic normal states, for the SIT and SMT systems, respectively.






